DL2 : Optimization in Deep Learning ~ Gradient Descent Strategies

Neural networks are universal function approximators. This means that with suffcient neurons, they can approximate any function (convex or not) well. Learning problems can be formulated and modelled as non-convex optimization, where a global minimum may not necessariliy be the local minimum. In achieving this, many convex optimization techniques such as stochastic gradient descent (SGD), mini-batching, and momentum are used. However, convergence to a bad local minimum may happen and the system will have to be re-optimized with a different sset of initialization and weights.A key question deep learning seeks to address then is - how fast can we find the optimal parameters?

In gradient descent, one goes through all the points from the training set before updating the parameters. The key parameter of this algorithm is the learning rate. If the learning rate is set to a huge or high number, then it may overshoot the local minima and if its set to a small/ low number, it will take a long time to converge. SGD always takes a noisy random path and the parameters always oscillate as visually described in the image below. The gradient of the loss function at the current step is iterated over multiple loops and is used to guide the search and determine the direction to go.

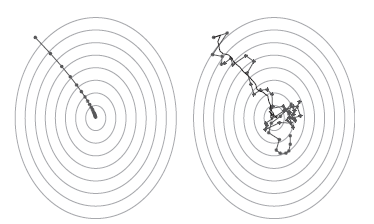
Direction Comparison between SGD and GD

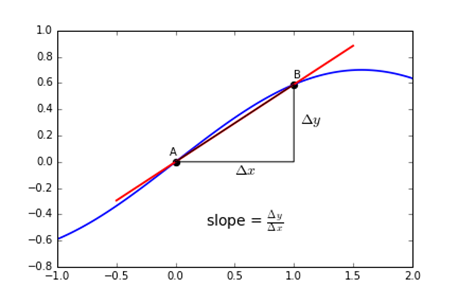
Backpropagation finds derivatives of the network by chain rule, multilpying the gradient of the network by moving from the final layer to the initial layer one by one. A small gradient means that weights and biases of the initial layers will not be updated effectively as we propagate downwards. This results in the model prematurely converging to a poor solution. The direction downwards to a given point is given by its derivative which is specified by the tangent line as seen in the image.

One way to get around this is to use the weight initialization scheme or alternative variants of the gradient descent activation functions such as Relu instead of sigmoid.

This is how batch gradient descent looks like in code :

for i in range(nb_epochs):
  params_grad = evaluate_gradient(loss_function, data, params)
  params = params - learning_rate * params_grad